Oj, nie jestem fanką piłki nożnej.
Zdarza mi się jednak obejrzeć mecz, zwykle mecz półfinałowy lub finałowy dużej piłkarskiej imprezy.
I oprócz podekscytowania grą, strzelonymi (lub nie) bramkami, czasem trudnym (dla mnie, choć może nie tylko dla mnie) do wychwycenia „spalonym”, interesuje mnie oczywiście kontekst matematyczny meczu piłkarskiego.
Nie byłoby meczu piłki nożnej, gdyby nie piłka właśnie. Kazimierz Górski, trener polskiej kadry w latach siedemdziesiątych ubiegłego wieku, mówił „piłka jest okrągła, a bramki są dwie”. Okrągła piłka. Czyli jak powstała? Jaki kształt wycięto z materiału, że powstała piłka?
Matematyka jest wszędzie.
Kształt piłek futbolowych związany jest z geometrią przestrzenną. Matematycznym modelem klasycznej piłki nożnej jest dwudziestościan ścięty, który składa się z 12 pięciokątów foremnych[1] i 20 sześciokątów foremnych. Taka piłka ma aerodynamiczny kształt uzyskany przez połączenie (zszycie lub sklejenie lub zgrzanie) 32 łatek.
[1] Wielokąt foremny to taki wielokąt, który ma wszystkie boki równe i wszystkie kąty wewnętrzne jednakowej miary.
Zdjęcie pochodzi ze strony: https://pl.wikipedia.org/wiki/Dwudziesto%C5%9Bcian_%C5%9Bci%C4%99ty
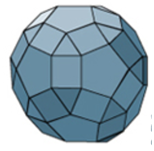
W 1997 roku zaprojektowano (firma Adidas, która dostarcza piłki na kolejne mistrzostwa) piłkę zbudowaną z trzech rodzajów wielokątów foremnych: 20 trójkątów równobocznych, 30 kwadratów i 12 pięciokątów foremnych.
Zdjęcie pochodzi ze strony:https://encyklopedia.pwn.pl/haslo/wieloscian;3995827.html
Na Euro 2020 taka właśnie „konstrukcja” piłki została wykorzystana.
„… a bramki są dwie”, a jeśli są bramki, to muszą być w nich zamontowane siatki. Dopatrzyłam się dwu rodzajów siatek: o oczkach kwadratowych i oczkach w kształcie sześciokątów foremnych tzw. „plastra miodu” (heksagonalna), jest także siatka, której oczka są trójkątami równobocznymi. Czyli klasyczny, matematyczny parkietaż (parkietaż platoński).
Zdjęcia pochodzą ze strony: https://allegro.pl/oferta/fototapeta-dziecko-pilka-w-siatce-nozna
I na koniec zachęcam do zweryfikowania tzw. paradoksu dnia urodzin. Wiąże się on z rozwiązaniem problemu: Ile minimalnie osób należy losowo wybrać, żeby prawdopodobieństwo znalezienia wśród nich co najmniej dwu osób obchodzących urodziny tego samego dnia było większe niż 0,5?
Czy Państwo wiecie, że wystarczą zaledwie 23 osoby (rachunek prawdopodobieństwa nie pozostawia wątpliwości).
Czyli, gdy na boisku mamy dwie piłkarskie drużyny i sędziego (co daje 23 osoby), szansa, że wśród nich będą dwie osoby obchodzące urodziny tego samego dnia jest nieco większa niż 50%.
19 czerwca na stadionie w Sewilli, na obiekcie Estadio La Cartuja, odbył się mecz między drużynami Polski i Hiszpanii (remis 1 :1). Przeanalizowałam daty urodzin wszystkich piłkarzy, którzy wyszli na murawę i okazuje się, że Jakub Moder i Gerard Moreno świętują urodziny 7 kwietnia, a Tymoteusz Puchacz i Karol Świderski, 23 stycznia.
Czy matematyka nie jest piękna?
„Bo dobry mecz to piękna rzecz
Wśród wielu szans Twoja jest”
Życząc słonecznych dni, wypoczynku i radości z codzienności, dostrzegajmy to, co nie zawsze jest oczywiste, dajmy sobie szansę.
Cudownych wakacji dla Państwa!
Lidia Okrzesa
nauczyciel doradca metodyczny z matematyki
Wykorzystałam:
https://www.google.com/search?client=firefox-b-d&q=futbol+futbol+futbol+prze%C5%BCyjmy+to+jeszcze+raz
https://pl.wikipedia.org/wiki/Pi%C5%82ka_no%C5%BCna
https://pl.wikipedia.org/wiki/Dwudziesto%C5%9Bcian_%C5%9Bci%C4%99ty
https://pl.wikipedia.org/wiki/Pi%C5%82ka_(pi%C5%82ka_no%C5%BCna)
https://pl.wikipedia.org/wiki/Paradoks_dnia_urodzin